Analyse des données IdFM

Author

Etienne Côme, Thomas Bapaume

Exemple de première analyse différenciée pré / post covid

Dans ce notebook, nous allons faire quelques analyses sur les données de fréquentations journalières.

# import de données
library(readr)
library(tools)
# manipulation de donénes
library(dplyr)
library(tidyr)
# travail sur les dates
library(lubridate)
# travail sur les chaines de caratcères
library(lubridate)
# visualisation
library(ggplot2)
library(ggtext)
#library(ggspatial)
# données spatiales
library(sf)
# bspline 
library(splines)
# regression sparse
library(Matrix)
library(glmnet)

Donnees calendaires et exemple de creation de variables

Pour commencer, nous allons récupérer des informations calendaires jours fériés / vacances … et compléter notre base de données en créant quelques variables intéressantes, validations a J-7, week-end, jour de l’année, jour de la semaine,…

# lecture des données nettoyées
data.val.ok=readRDS("./data.val.ok.RDS") |>
    mutate(LOG_VAL = log(NB_VALD),year=year(JOUR),yd=yday(JOUR),wd=wday(JOUR)) 
# statistiques globales
st_glob_stats = data.val.ok |>  
  group_by(ID_REFA_LDA,NAME) |>
  summarise(M_VALD=mean(NB_VALD),NB_VALD = sum(NB_VALD),NB_J=n()) |> 
  arrange(desc(NB_VALD)) 

download.file("https://www.data.gouv.fr/fr/datasets/r/6637991e-c4d8-4cd6-854e-ce33c5ab49d5",destfile = "./data-raw/jf.csv")
feries = read_delim("./data-raw/jf.csv") |> filter(zone=="Métropole")

download.file("https://raw.githubusercontent.com/AntoineAugusti/vacances-scolaires/master/data.csv",destfile = "./data-raw/vacances.csv")
vacances = read_csv("./data-raw/vacances.csv") |> filter(vacances_zone_c) |> select(date,nom_vacances)



selected_ids = st_glob_stats |> ungroup() |> head(100) |> pull(ID_REFA_LDA)
#selected_ids = st_glob_stats |> filter(M_VALD>500)|> pull(ID_REFA_LDA)
N=length(selected_ids)

data.cal = data.val.ok |> 
  filter(ID_REFA_LDA %in% selected_ids)  |> 
  mutate(feries=JOUR %in% feries$date,vacances=JOUR %in%vacances$date) |>
  mutate(weekend=wd==6|wd==0) |> 
  mutate(JOUR_lag7=JOUR-7) |>
  rename(id=ID_REFA_LDA)

data.cal.lag = data.cal |> 
  select(JOUR,id,LOG_VAL,NB_VALD) |> 
  rename(JOUR_lag7=JOUR,LOG_VAL_lag7=LOG_VAL,NB_VALD_lag7=NB_VALD)
data.lag = data.cal |> 
  left_join(data.cal.lag) |> 
  filter(!is.na(LOG_VAL_lag7))

Exemple de modèle de régression

Pour analyser les fréquentations, nous allons construire un modèle de référence sur la période pré-pandémie. Nous allons utiliser un modèle log-linéaire du type :

model_formula=LOG_VAL~factor(wd)*id+feries+bs(yd,30)

Ce modèle explique le logarithme du nombre de validation, avec un effet des jours de la semaine (wd) qui dépend de la station, un effet jours fériés commun à toutes les stations et enfin un motif annuel (yd) également commun à toutes les stations.

Nous allons tester ce modèle pour 4 stations avant de l’utiliser pour l’ensemble:

# filtrage des données 
train.df = data.lag |> filter(year<=2018 , id %in% c("482368")) 
fit_small = lm(LOG_VAL~factor(wd)+feries+bs(yd,24)-1,train.df)
gtsummary::tbl_regression(fit_small)

Characteristic	Beta	95% CI¹	p-value
factor(wd)
1	7.6	7.2, 7.9	<0.001
2	8.9	8.6, 9.2	<0.001
3	9.0	8.7, 9.4	<0.001
4	9.1	8.7, 9.4	<0.001
5	9.1	8.8, 9.5	<0.001
6	9.1	8.7, 9.4	<0.001
7	8.7	8.3, 9.0	<0.001
feries
FALSE	—	—
TRUE	-0.83	-0.98, -0.69	<0.001
bs(yd, 24)
bs(yd, 24)1	0.61	-0.02, 1.2	0.058
bs(yd, 24)2	0.62	0.21, 1.0	0.003
bs(yd, 24)3	0.55	0.08, 1.0	0.021
bs(yd, 24)4	0.44	0.03, 0.85	0.034
bs(yd, 24)5	0.35	-0.08, 0.78	0.11
bs(yd, 24)6	0.45	0.03, 0.86	0.036
bs(yd, 24)7	0.20	-0.22, 0.63	0.4
bs(yd, 24)8	0.60	0.18, 1.0	0.005
bs(yd, 24)9	0.20	-0.22, 0.62	0.4
bs(yd, 24)10	0.46	0.05, 0.88	0.029
bs(yd, 24)11	0.44	0.02, 0.86	0.041
bs(yd, 24)12	0.40	-0.02, 0.81	0.060
bs(yd, 24)13	0.67	0.26, 1.1	0.002
bs(yd, 24)14	0.51	0.08, 0.93	0.019
bs(yd, 24)15	0.33	-0.10, 0.76	0.13
bs(yd, 24)16	-0.31	-0.73, 0.10	0.14
bs(yd, 24)17	0.45	0.03, 0.87	0.037
bs(yd, 24)18	0.40	-0.02, 0.82	0.063
bs(yd, 24)19	0.53	0.11, 0.96	0.014
bs(yd, 24)20	0.44	0.02, 0.86	0.041
bs(yd, 24)21	0.57	0.13, 1.0	0.011
bs(yd, 24)22	0.17	-0.33, 0.68	0.5
bs(yd, 24)23	1.2	0.69, 1.7	<0.001
bs(yd, 24)24	-0.30	-0.80, 0.19	0.2
¹ CI = Confidence Interval

pattern_annuel=data.frame(yd=1:366,pann=predict(fit_small,data.frame(yd=1:366,wd=factor(rep(2,366,levels=1:7)),feries=rep(FALSE,366))))
ggplot(pattern_annuel)+geom_line(aes(x=as.Date("01/01/2015",format="%d/%m/%Y")+yd,y=exp(pann)))+scale_y_continuous("Composante annuelle",limits=c(0,15250))+scale_x_date("Mois",date_breaks = "months",date_labels="%m")+theme_bw()+labs(title="Composante annuelle")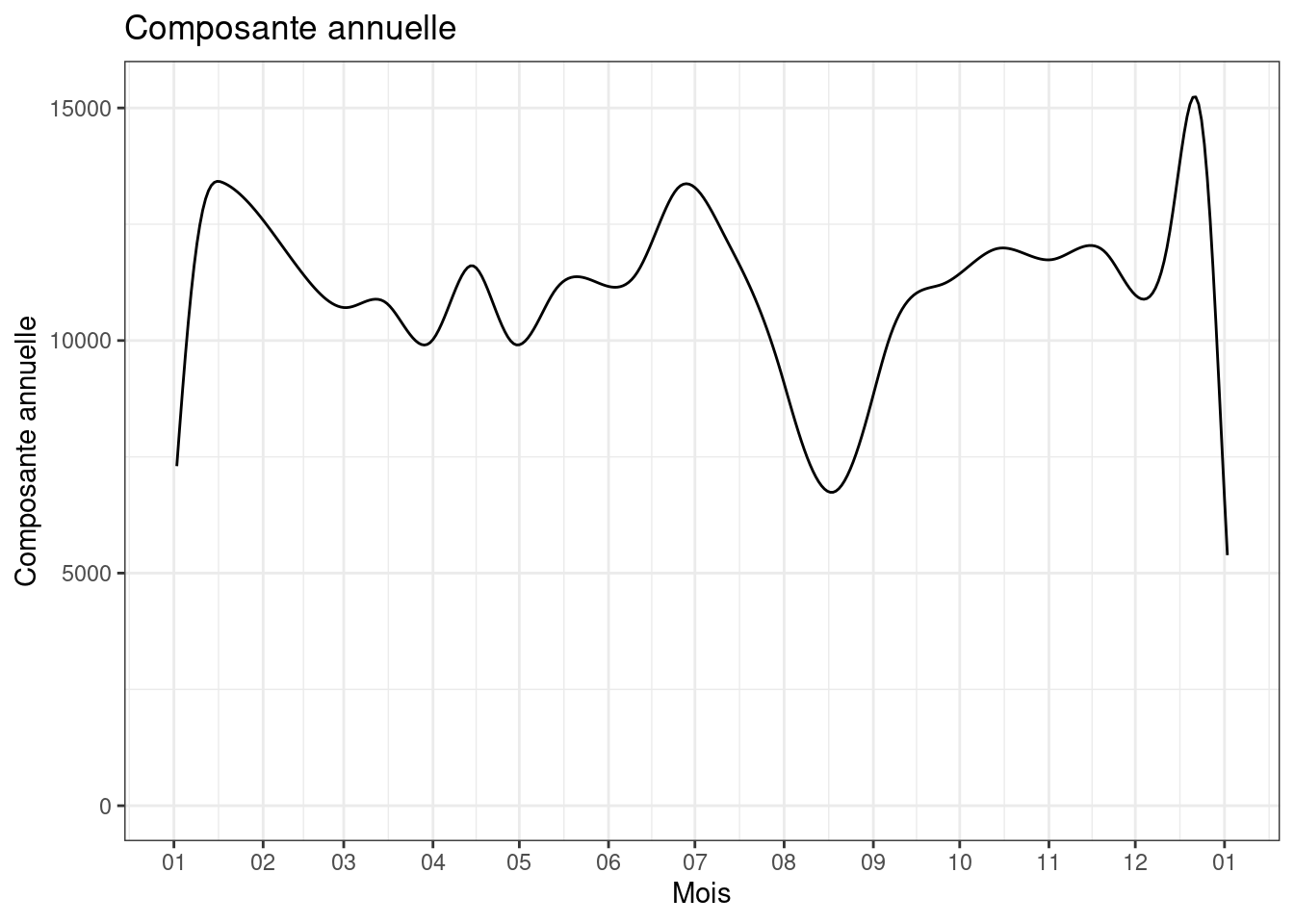

# filtrage des données 
train.df = data.lag |> filter(year<=2018)
# creation de la matrice sparse
Xapp = sparse.model.matrix(model_formula,data=train.df)
# estimation
fit=glmnet(y=train.df$LOG_VAL,x=Xapp,familly="gaussian")
# prediction
yh=predict(fit,Xapp)
# residus
train.df$residuals=train.df$LOG_VAL-yh[,ncol(yh)]
train.df$NB_VAL_PRED=exp(yh[,ncol(yh)])
ids = unique(train.df$id)
subset = ids[sample(N,4,replace = FALSE)]

ggplot(train.df |> filter(id %in% subset,year==2016)) +
  geom_line(aes(x=JOUR,y=NB_VALD),alpha=0.8,color="#4daf4a") + 
  geom_line(aes(x=JOUR,y=NB_VAL_PRED),alpha=0.8,color="#ee5555") + 
  facet_wrap(~paste(NAME,id))+
  labs(title="Volumes <span style='color:#ee5555'>prédits</span> et <span style='color:#4daf4a'>observés</span>",
       subtitle="pour une selectionde stations en 2016",y="Nombre de validations",x="Date",caption = "source: données historique de validations IdFM")+
  theme_bw()+
  theme(plot.title = element_markdown())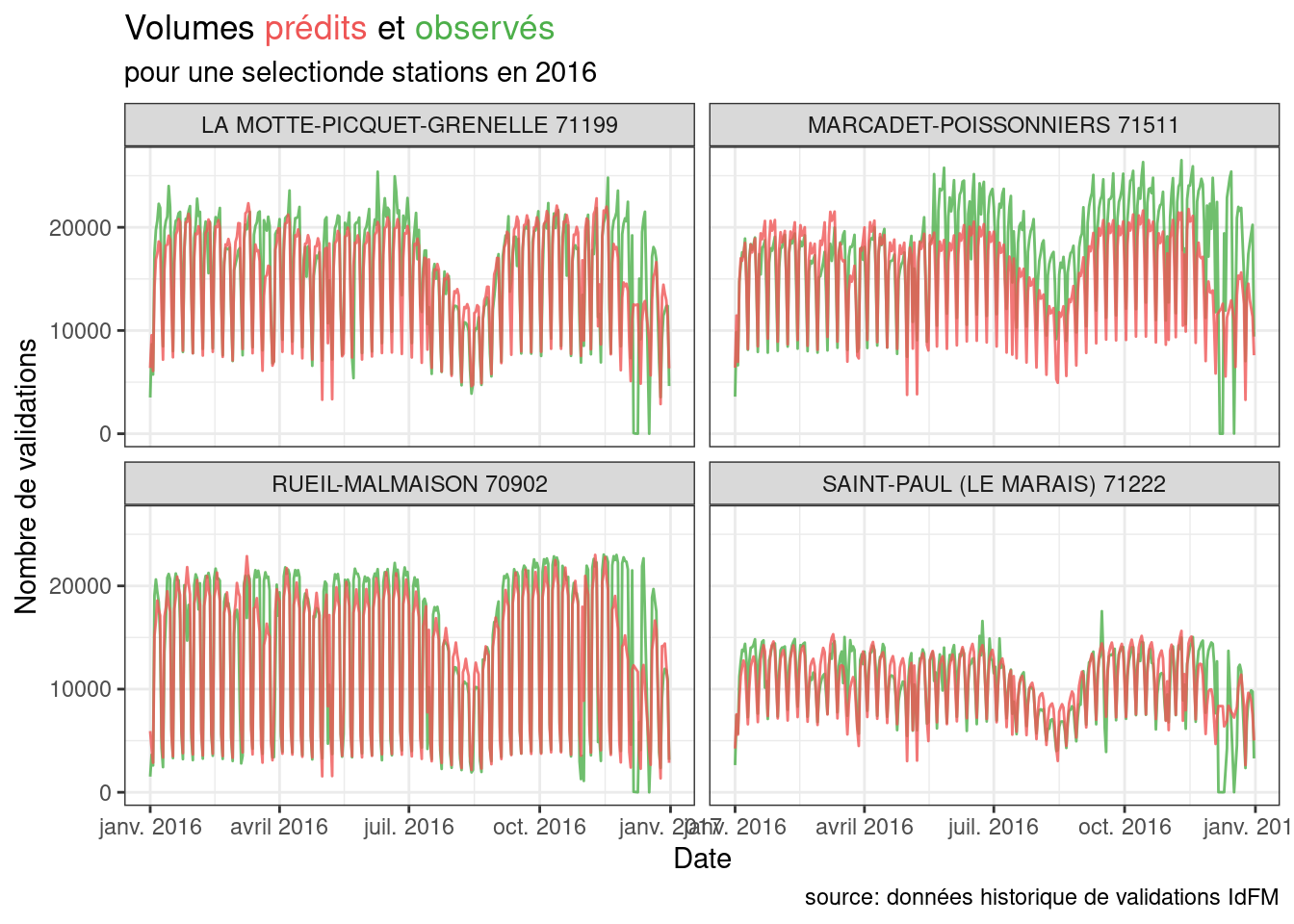

ggplot(train.df |> filter(id %in% subset,year==2017)) +
  geom_line(aes(x=JOUR,y=residuals,group=paste(year,id)),alpha=0.5) + 
  facet_wrap(~paste(NAME,id))+
    labs(title="Résidus sur les données d'apprentissage",
       subtitle="pour une selectionde stations en 2017",y="log-résidus",x="Date",caption = "source: données historiques de validations IdFM")+
  theme_bw()+
  theme(plot.title = element_markdown())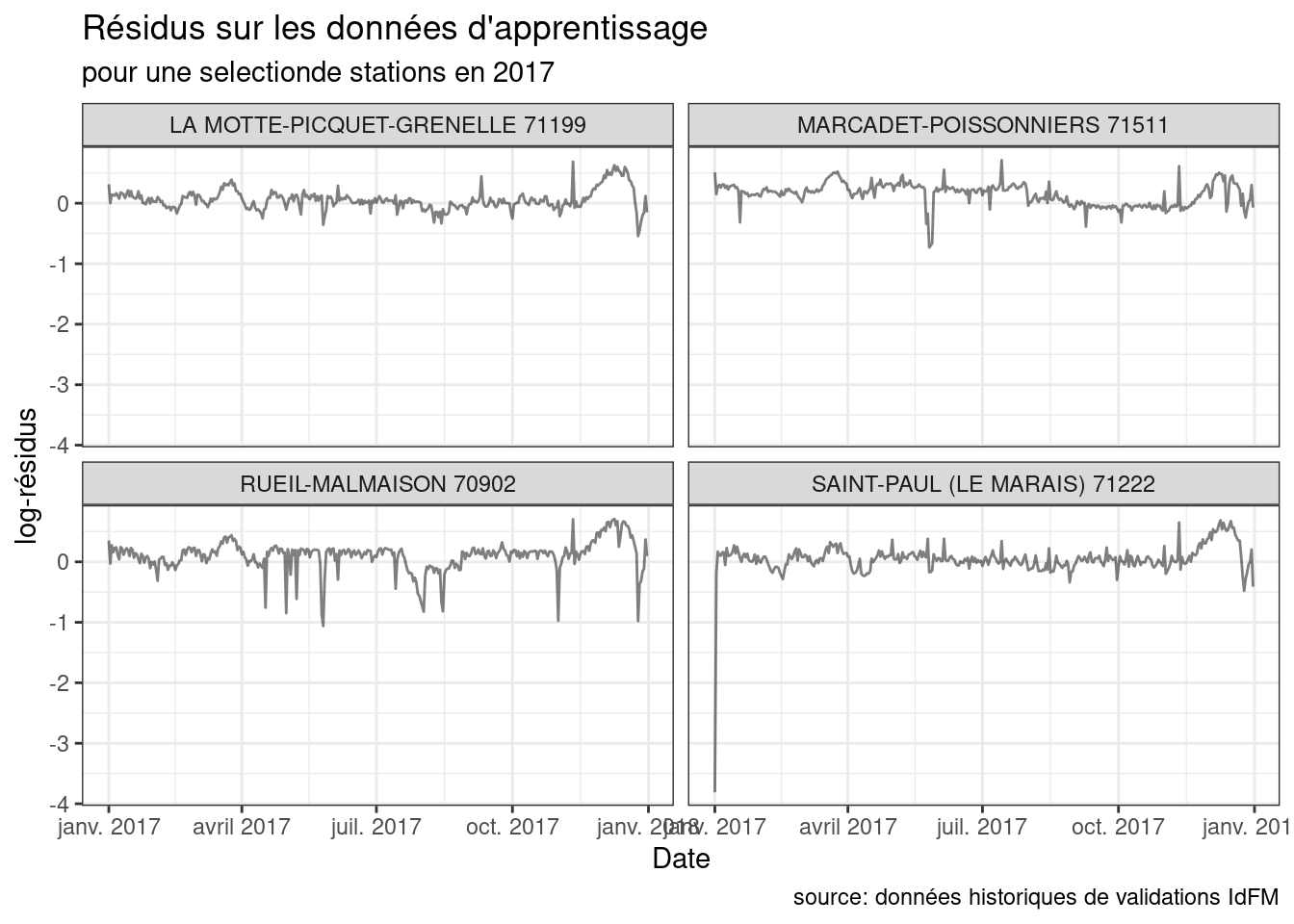

Utilisation du modèle nominale pour analyser les données post-covid

Suppression des greves / jours atypiques

Un certains nombre de jours sont très atypiques dans cette base de données d’apprentissage (grêves, …).

res.glob = train.df |> 
  group_by(JOUR,feries) |> 
  summarise(mres=mean(residuals))

ggplot(res.glob,aes(x=JOUR,y=mres))+
  geom_line()+
  geom_point(data=res.glob|>filter(feries),color="#4daf4a")+
  geom_point(data=res.glob|>filter(abs(mres)>2),color="#ee5555")+
  labs(title="Moyenne des résidus par jour",
       subtitle="les <span style='color:#4daf4a'>jours ferriés</span> et <span style='color:#ee5555'>jours atypiques</span> sont mis en évidence",x="log-résidus moyen",y="Date",caption = "source: données historiques de validations IdFM")+
  theme_bw()+
  theme(plot.subtitle = element_markdown())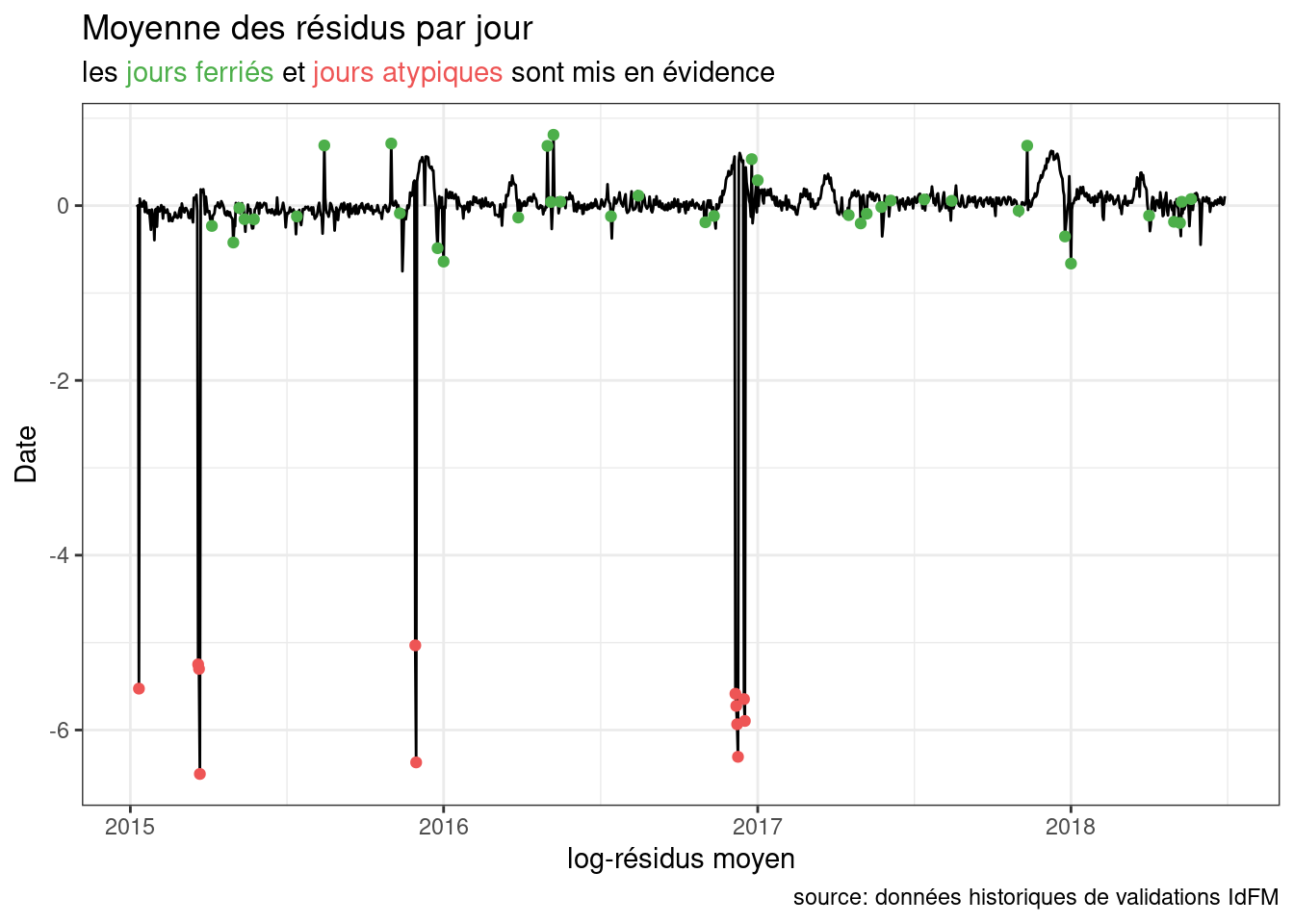

Pour ne pas que ceux-ci influencent le modèle nominale, nous allons les filtrer et ré-effectuer l’apprentissage sans ceux-ci.

greves = res.glob$JOUR[res.glob$mres<(-2)]
train.df.filtered = train.df |> filter(!JOUR %in% greves) 
Xapp.filtered = sparse.model.matrix(model_formula,data=train.df.filtered)
fit=glmnet(y=train.df.filtered$LOG_VAL,x=Xapp.filtered,familly="gaussian")
yh=predict(fit,Xapp.filtered)
train.df.filtered$residuals=train.df.filtered$LOG_VAL-yh[,ncol(yh)]

La régression utilisée et une régression avec pénalité L1, nous allons nous servir d’un ensemble de validation pour choisir une valeur de pénalisation.

val.df=data.lag |> 
  filter(year==2019, month(JOUR)<=6)

Xval = sparse.model.matrix(model_formula,data=val.df)
err=sapply(1:length(fit$lambda),\(l){
  mean((val.df$LOG_VAL-predict(fit,Xval,fit$lambda[l]))^2)
})

sel.lambda = data.frame(mse=err,lambda=fit$lambda,i=1:length(err))
ggplot(sel.lambda,aes(x=log(lambda),y=mse))+
  geom_line()+
  theme_bw()+
  labs(x="Lambda",y="Erreur quadratique moyenne",
       title="Performances sur les données de validations",
       subtitle="en fonction de lambda")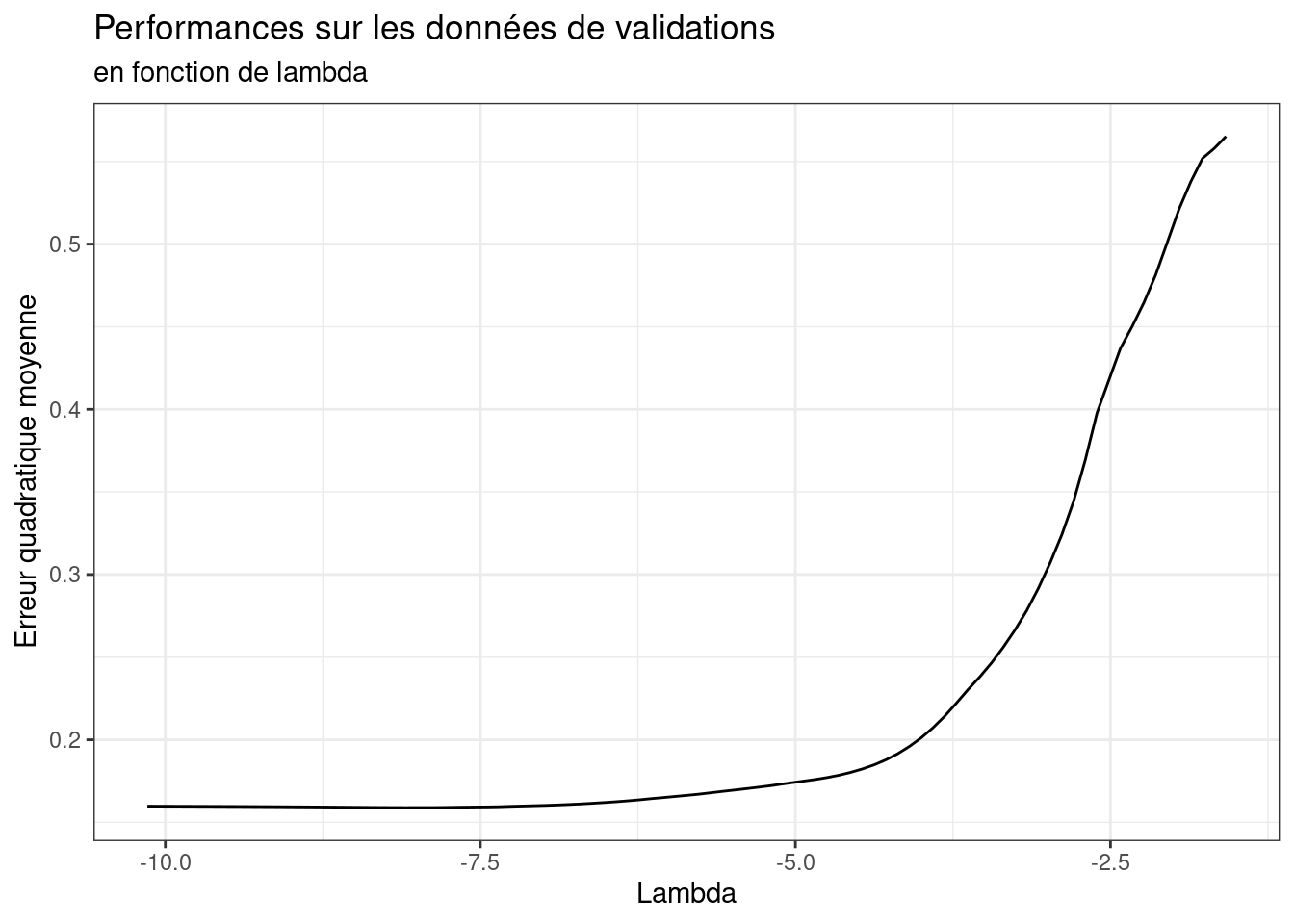

l_opt=which.min(err)

Nous allons maintenant nous servir de ce denier modèle pour retirer des données post-covid les variations attendues par le modèle pré-covid.

test.df = data.lag |> 
  filter(JOUR>as.Date("01/07/2019",format="%d/%m/%Y"))
Xtst= sparse.model.matrix(model_formula,data=test.df)
test.df$residuals=test.df$LOG_VAL-predict(fit,Xtst,s=fit$lambda[l_opt])

Cela va nous permettre d’analyser les résidus, i.e ce qui a changé depuis la pandémie:

subset = ids[sample(N,12,replace = FALSE)]
gg = test.df|> filter(id%in% subset) |> filter(year==2022)
ggplot(gg) +
  geom_line(aes(x=JOUR,y=residuals,group=id),alpha=0.5)+
  geom_point(data=gg |> filter(feries),aes(x=JOUR,y=residuals),color="red",size=0.3)+
  facet_wrap(~paste(id,NAME))+
  scale_color_discrete(guide="none")+
  scale_y_continuous(limits=c(-2.5,1.5))+
  theme_bw()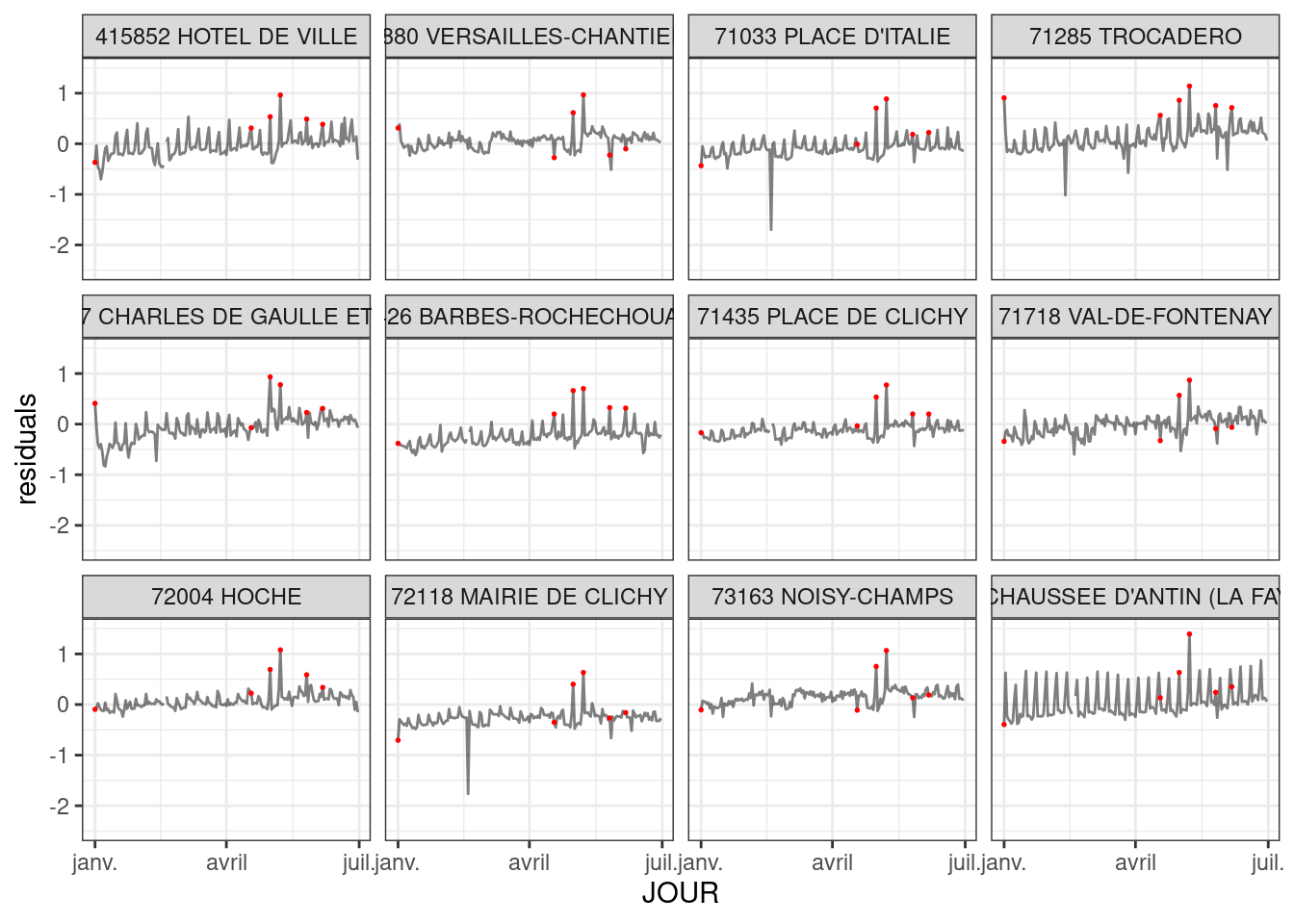

En nous focalisant sur une station et sur 2022:

selected.df = test.df|> filter(id=="482368",year>=2022)
ggplot(selected.df,aes(x=JOUR,y=residuals,group=id,label=format(JOUR,"%d/%m/%Y"))) +
  geom_hline(yintercept=0,linewidth=1.5,col="#555555",alpha=0.3)+
  geom_line(alpha=0.5)+
  geom_point(data=selected.df |> filter(feries),color="#4daf4a")+
  facet_wrap(~paste(NAME,id))+
  geom_point(data=selected.df|>filter(abs(residuals)>1&!feries),col="#ee5555")+
  geom_text(data=selected.df|>filter(abs(residuals)>1&!feries),vjust=-1)+
  scale_color_discrete(guide="none")+
  labs(title="Résidus par jour",
       subtitle="les <span style='color:#4daf4a'>jours ferriés</span> et <span style='color:#ee5555'>jours atypiques</span> sont mis en évidence",y="log-résidus",y="Date",caption = "source: données historiques de validations IdFM")+
  theme_bw()+
  theme(plot.subtitle = element_markdown())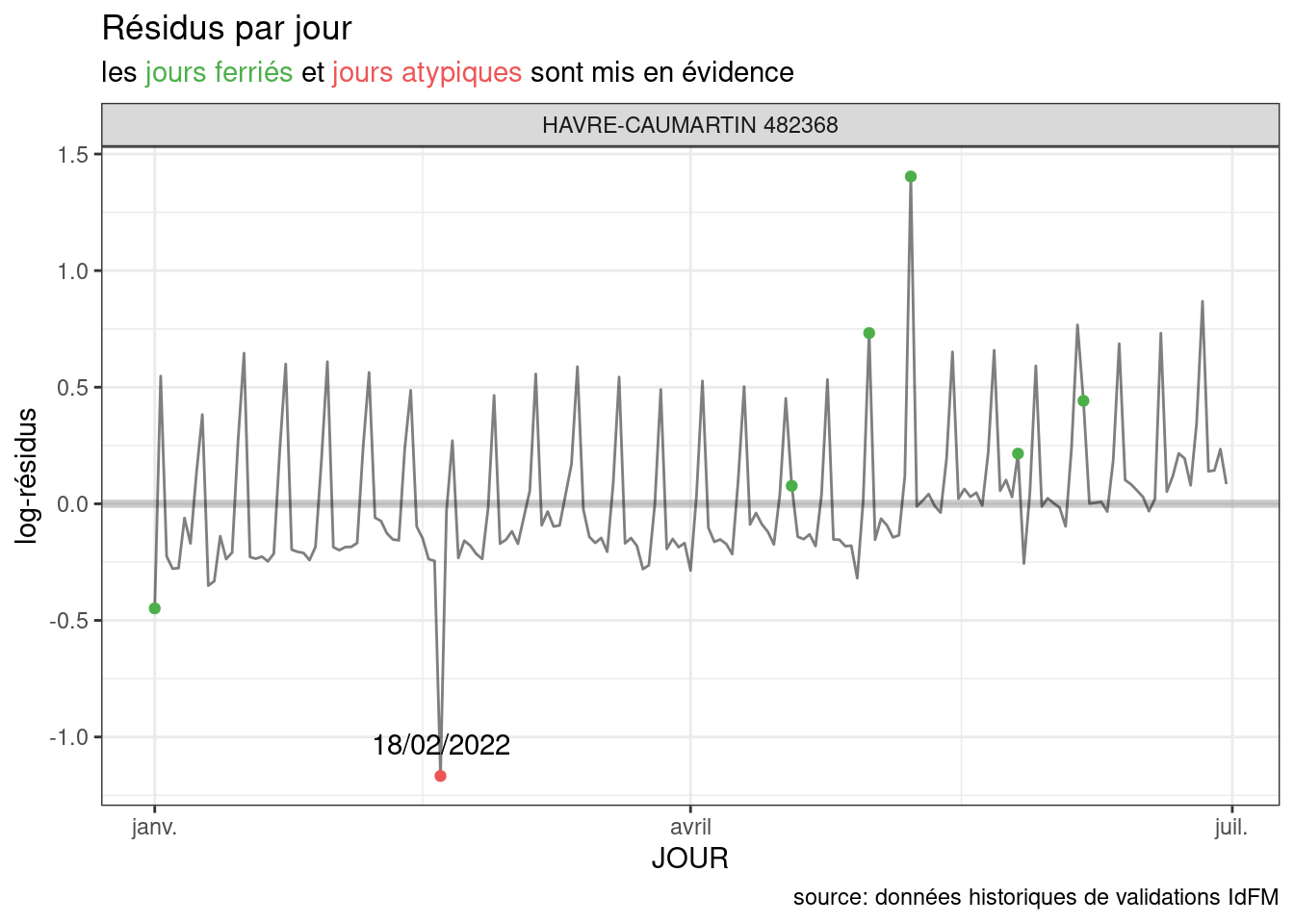

Nous pouvons souvent observer un pattern hebdomadaire dans ceux-ci. Ce que nous pouvons confirmer avec une régression.

selected.df=selected.df |>filter(!feries,abs(residuals)<1)
fit_res_wd = lm(residuals ~ factor(wd)-1,data=selected.df)
gtsummary::tbl_regression(fit_res_wd)

Characteristic	Beta	95% CI¹	p-value
factor(wd)
1	0.57	0.52, 0.62	<0.001
2	-0.10	-0.15, -0.05	<0.001
3	-0.09	-0.13, -0.04	<0.001
4	-0.09	-0.14, -0.05	<0.001
5	-0.11	-0.16, -0.07	<0.001
6	-0.16	-0.21, -0.11	<0.001
7	0.13	0.08, 0.17	<0.001
¹ CI = Confidence Interval

pred_days=predict(fit_res_wd,data.frame(wd=factor(1:7,levels = 1:7)))
lev=c("Dimanche","Lundi","Mardi","Mercredi","Jeudi","Vendredi","Samedi")
df.wd=data.frame(evol=round(exp(pred_days)-1,3)*100,wd=factor(lev,levels=c(lev[2:7],lev[1])))


ggplot(df.wd,aes(y=wd,x=evol,fill=evol))+geom_col()+
  theme_bw()+
  scale_fill_distiller(palette="RdBu",breaks=c(-15,-5,0,5,50),values=scales::rescale(c(-15,-5,0,5,50)))+
  labs(x="Evolution (%) par rapport à la période prè-COVID",y="",title="Evolution de la fréquentation suivant le type de jour")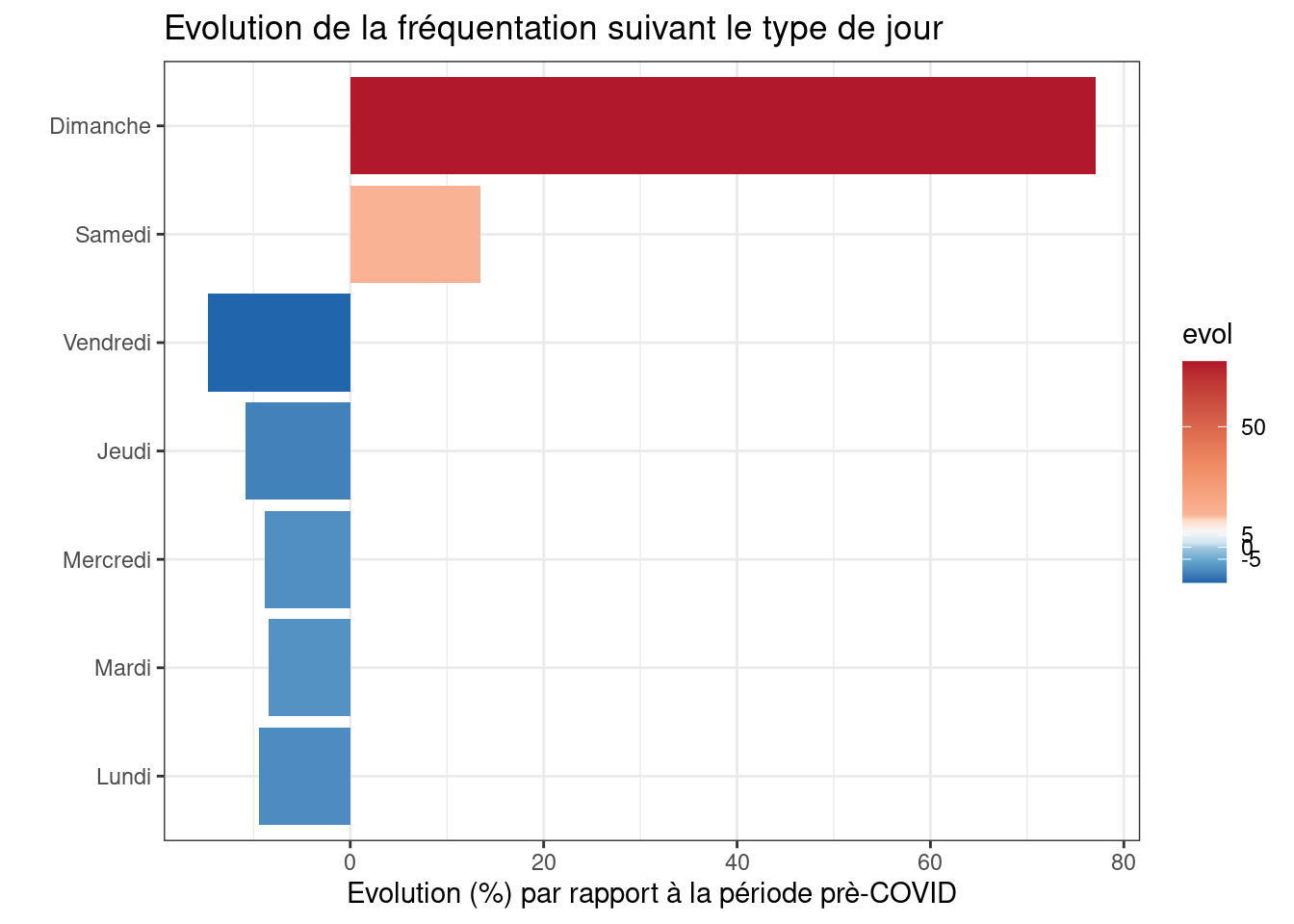

conf_intervals=round((exp(confint(fit_res_wd,level=0.95))-1)*100,1)
df.wd=cbind(df.wd,conf_intervals)

ggplot(df.wd)+geom_errorbar(aes(x=wd,ymin=`2.5 %`,ymax=`97.5 %`))+
  geom_hline(yintercept=0,color="red")+
  geom_point(aes(x=wd,y=evol))+
  labs(y="Evolution en % par rapport au modèle pré-covid",x="Jour de la semaine",title="Evolution en % par rapport au modèle pré-covid")+
  theme_bw()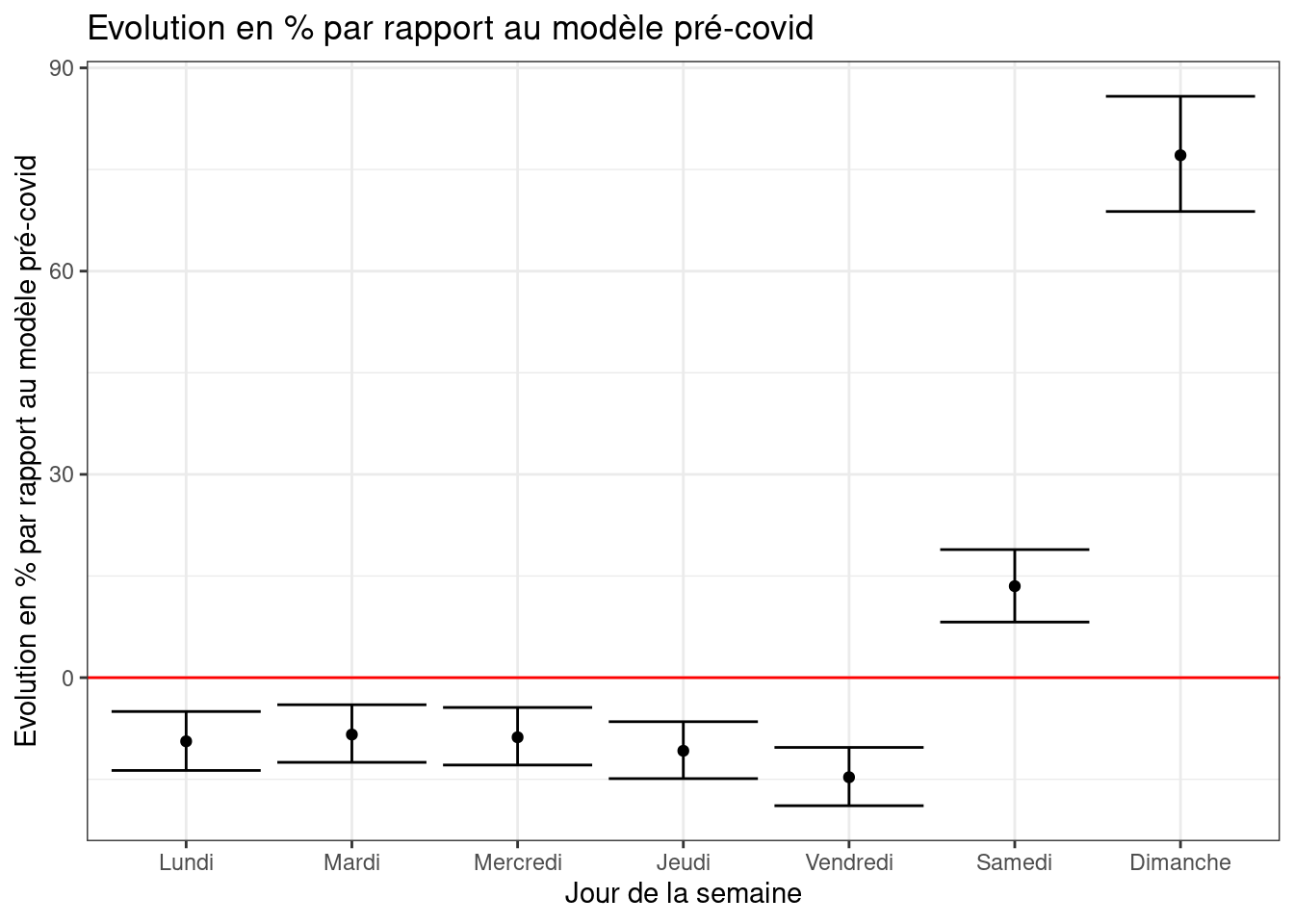

gg.cal=selected.df |> mutate(y=forcats::fct_rev(wday(JOUR,label=TRUE,week_start = 1))) |>
  mutate(x=week(JOUR),md=mday(JOUR),month=month(JOUR,label=TRUE)) |>
  select(x,y,md,month,year,residuals)

col_scale_vals = c(seq(min(gg.cal$residuals),0,length.out=5)[1:4],0,seq(0,max(gg.cal$residuals),length.out=5)[2:5])
month = gg.cal |> filter(md==1) |> filter(!duplicated(x)&!duplicated(month))

ggplot(gg.cal,aes(x=x,y=y,fill=residuals,label=md))+geom_tile(color="#000000")+
  coord_equal(expand = FALSE)+
  scale_fill_distiller("log-residuals",palette="RdBu",values=scales::rescale(col_scale_vals))+
  geom_text(size=2,hjust=-0.25,vjust=-0.25)+
  scale_x_continuous("",breaks=month$x,labels = month$month)+
  theme_bw()+
  facet_grid(year~.)+
  labs(y="",title="Calendrier des résidus")+
  theme(legend.position="bottom")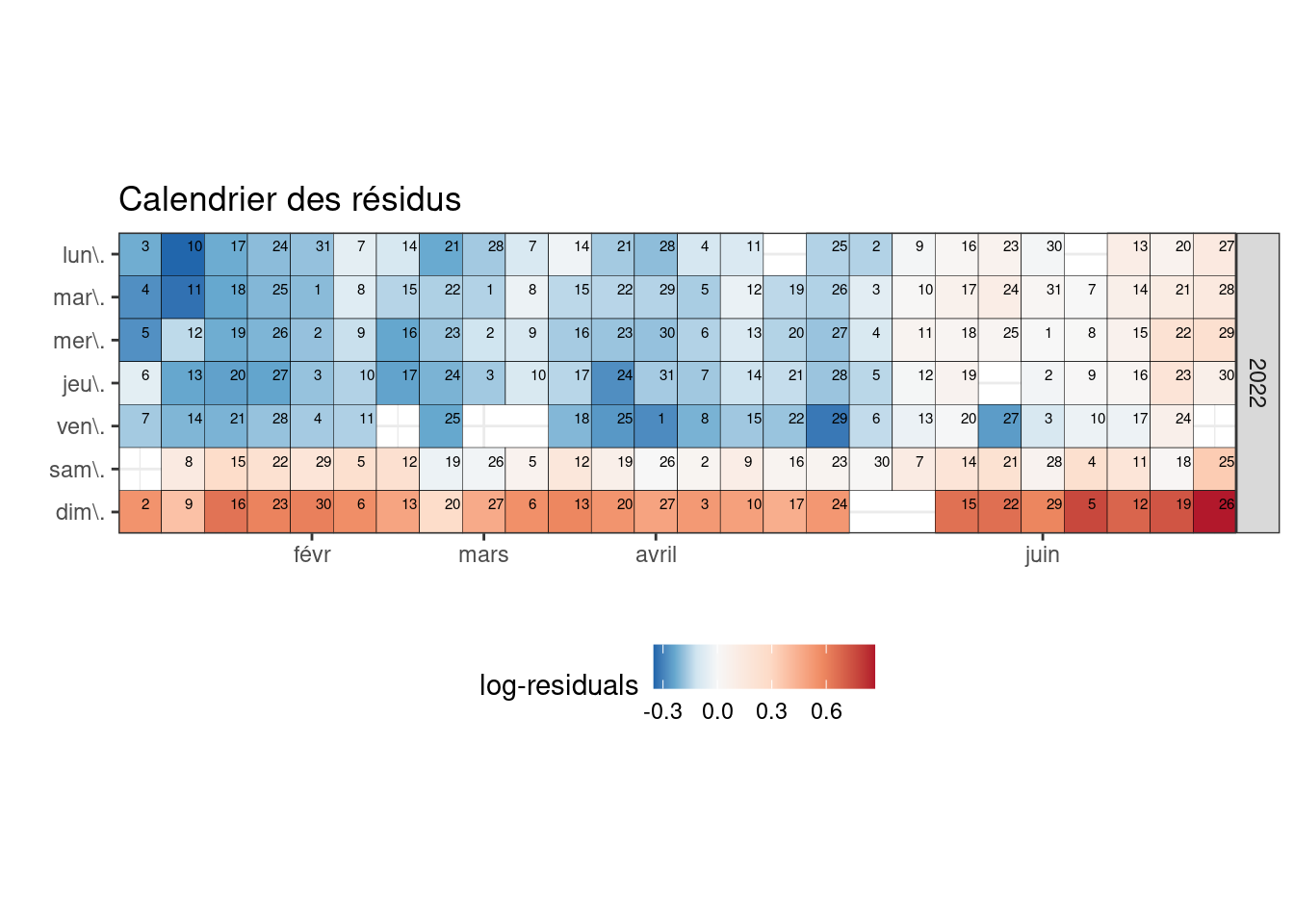

Application shiny

Pour explorer plus facilement ces résultats une petite application shiny est disponible, à vous de jouer !